When you buy through nexus on our site , we may bring in an affiliate commission . Here ’s how it works .
For many , the idea of math will bring in back endless hours of recipe and equations at schooling . So it may seem hard to imagine , but there once was a prison term when arithmetical did n’t live . Of course , there was still the need to utilise complex computing to solve real - world problems , but it was n’t until Muhammad ibn-Mūsā al-Khwārizmī , the so - bid " father of algebra , " established the first harmonic for solving equations that we began to set the foundations for modernmathematics .
In this excerpt from her new book " Vector : A Surprising Story of Space , Time , and Mathematical Transformation " , mathematicianRobyn Arianrhodexplores the 4,000 - year phylogeny of the language of mathematics — from complex descriptions to the symbolic form we cognize today .
Learning to think symbolically
Algebra has been part of mathematics since record began nearly 4,000 years ago , but not always in the symbolic build we learn today . In fact , for most of those four millennia it was written all in words and numeral — although works such as Euclid ’s famous 300 B.C.E. textbook " Elements " also included geometric diagrams , to assist evidence such things asPythagoras ’s theorem , and to show how to exposit squares that we would compose today as(a+b)2 .
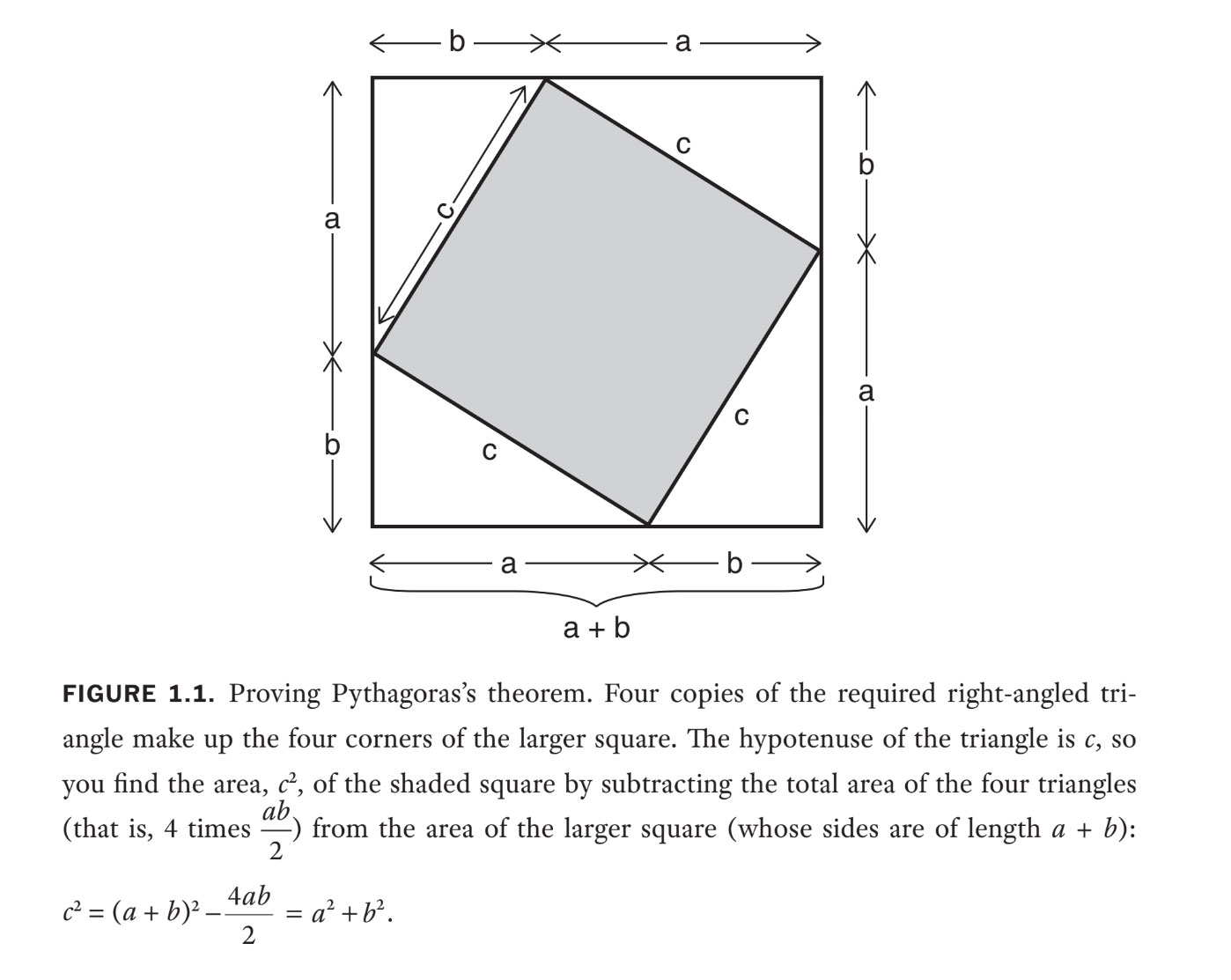
So " algebra " was communicated in cumbersome news problem or increasingly complicated diagrams — although geometry did have its advantages . For example , it ’s the easiest way to prove Pythagoras ’s theorem . In figure 1.1 , I ’ve devote an algebraical adaption of such a proof , although the ancient simply rearranged the diagram to show visually that the shaded country is equal to the sum of the areas of the squares on the adjacent sides of the triangle — a fairly apt approach !
It took a long clip for algebra to come forth from arithmetic and geometry as a separate subject . It did n’t even get its name until mediaeval times , and that was thanks to the ninth-century Persian mathematicianMuhammed ibn-Mūsā ( al-)Khwārizmī … He studied at Caliph al-Ma’mūn ’s pioneering Baghdad-based university , or " House of Wisdom , " when the heavy Arabic translation apparent movement was at its pinnacle : Greek , Indian , and other ancient manuscripts were being collected from all corners of the burgeon Islamic empire and translated into Arabic .
Imperialism is seldom honourable and often violent , but it can ultimately lead to ethnic cross-fertilization , and in this case the visionary rendering movement was so important that by the 12th century , Europeans were learning Arabic to translate these manuscripts into Latin — let in Ptolemy ’s " Almagest " and Euclid ’s " Elements , " along with new Arabic works such as those of al-Khwārizmī . The name " algebra ” famously amount from the first Holy Writ in the title of respect of his book " Al - Jabr wa’l muqābalah " — which means something like " The Compendious Book on Calculation by Completion and Balancing . "
pass judgment from the problems al-Khwārizmī included , an exercise of what he meant by " Completion " is " complete the lame , " the method you might have study in school to solve quadratic equations …
Al-Khwārizmī did n’t write equations in the symbolic form we use today , either . In fact , to New eyes his book is more arithmetical than algebraic , and one of its of import impacts in Europe , when it was translated into Latin , was the popularization of the Hindu-Arabic decimal system of count that finally evolved into our modern one .

Muhammad ibn Musa al-Khwarizmi
Yet Al-Khwārizmī is often called the " Church Father of algebra . " He may have used Book rather than symbols , and the problems he included may have been childlike — his design , he tells us , was to teach pupil how to solve basic problems in " vitrine of heritage , bequest , partitions , cause and trade wind , and in all their dealings with one another , or where the measuring of land , the digging of canal , geometric calculation , and other object of various sorts and kinds are concerned . "
But he systematically set out word-form linear and quadratic equations , with algorithmic methods for figure out them — that is , for finding the " nameless numbers , " our modernx ’s andy ’s . In fact , the English word " algorithm ” — have in mind a lot of rules for performing a calculation or other operation — occur from " algorismi , ” an early Latinized attempt at Al-Khwārizmī .
…
The beauty of symbolic equations is that it ’s much easier to see these general patterns when you’re able to see a job at a glance . equate this :
Take the foursquare of the unknown number ,
then add the strange number to itself

and take the sum away from the square ;
now let the total be eight .
with this :

x2–2x=8
And there ’s more : The earliest mathematician solved each equality separately , but it ’s leisurely if you’re able to see that whatever method works for the equationx2–2x=8will also work for any equation of the same form , x2 – axe = b. Eventually , ancient mathematician did begin to recognise this , but progress was comparatively dull because they had to keep all these convention in their head , or in long , convoluted conviction , and it was easy to miss track .
The first to write any equation in a transparent , recognizably modern symbolic form were[Thomas ] Harriot’sexecutors in 1631 , and then [ René ] Descartes in an appendix to his 1637 " Discourse on Method . " ( There were a few earlier attempts , but the symbolism — more right called abbreviation — was torment and idiosyncratic . ) Even the + , − , = , and × sign we take for granted only came into widespread use in the 17th century . Which means that the earlier algebraist we know of — the ancient Mesopotamians , Egyptians , Chinese , and Greeks , the medieval Indians , Persians , and Arabs , as well as the early modern Europeans — all had expressed their equivalence mostly in word or pictorial word images .

Related:9 equations that change the world
It is a singular accomplishment to think symbolically , as this long account shows . Take the Son problem I give above : it is an instance of algorithmic thought process . But symbolic thinking is algorithmic and more , for its symbols sometimes contain the seminal fluid of a new kind of creative thinking — a new kind of far-reaching yet economical thought .
A classical casing isAlbert Einstein’sE = mc2 . Einstein did not set out to receive the connection between energy and matter . Rather , he simply desire to calculate the energizing energy of a moving negatron according to his newtheory of relativity theory , so that his theoretical prevision could be tested by experimentation .

A few months later , however , 26-year-old Einstein begin to bring in the significance of his equation . He wrote it up in his fifth groundbreaking ceremony paper of 1905 , his annus mirabilis , but it would take him two more geezerhood to tease out the full , spectacular implication of this symbolic relationship . To realize that this was n’t just a computing about a particular physical body of Energy Department and a particular type of affair , it was general : if a body gain ( or fall back ) vim , it also gains ( or lose ) mass . This bizarre idea is alien to all our commonsense experience — but there it was , hide in the symbols of his equating . It took data-based physicist decades to by experimentation support this staggering mathematical prediction .
A much simple and early example is the sequence of powersx , x2,x3and so on . The first " power " is 1 , soxis reallyx1 , where the 1 was traditionally link geometrically to a 1-D credit line . The next two , x2andx3 , are pronounced " x square " and " x cubed " by analogy with the area of a square and the bulk of a cube . These names highlight the way that other mathematician thought geometrically rather than algebraically , because of the real nature of geometry . By contrast , symbolic algebra is nonobjective : you have to give it import , even if it is merely the display of an interesting pattern such asx , x2 , x3 , x4, … But this flexibility is algebra ’s great forte . you could pen down as many ( finite ) higher powers as you care , without having to visualize them as strong-arm physical object .
— What is the turgid known prize number ?

— The 9 most massive telephone number in existence
— ' The most magical equation in physics ' : How Paul Dirac unintentionally revealed the unknown worldly concern of antimatter
This may sound obvious today , but it took three and a half thousand age for mathematicians to move from solving quadratic equations — " quadratic " derives from the Latin for " square , " so quadratic equations are those whose highest powerfulness isx2(the unknown reproduce by itself , as the antediluvian put it ) — to solving " three-dimensional " and higher equations . These higher - degree equations are much more difficult , of path ; but part of the cause resolution did n’t come easy was that algebra was splice to word and concrete images for such a very long time .

For example , I mentioned Al-Khwārizmī ’s " completing the square " in orderliness to resolve a quadratic equation . It ’s actually a 4,000-year-old problem , dating back ( as far as the historic phonograph recording show ) to cuneiform tablets made by mathematicians living , like Al - Khwārizmī , in the region of modern-day Iraq . These ancient Mesopotamians solve quadratic equations by literally fill out a square .
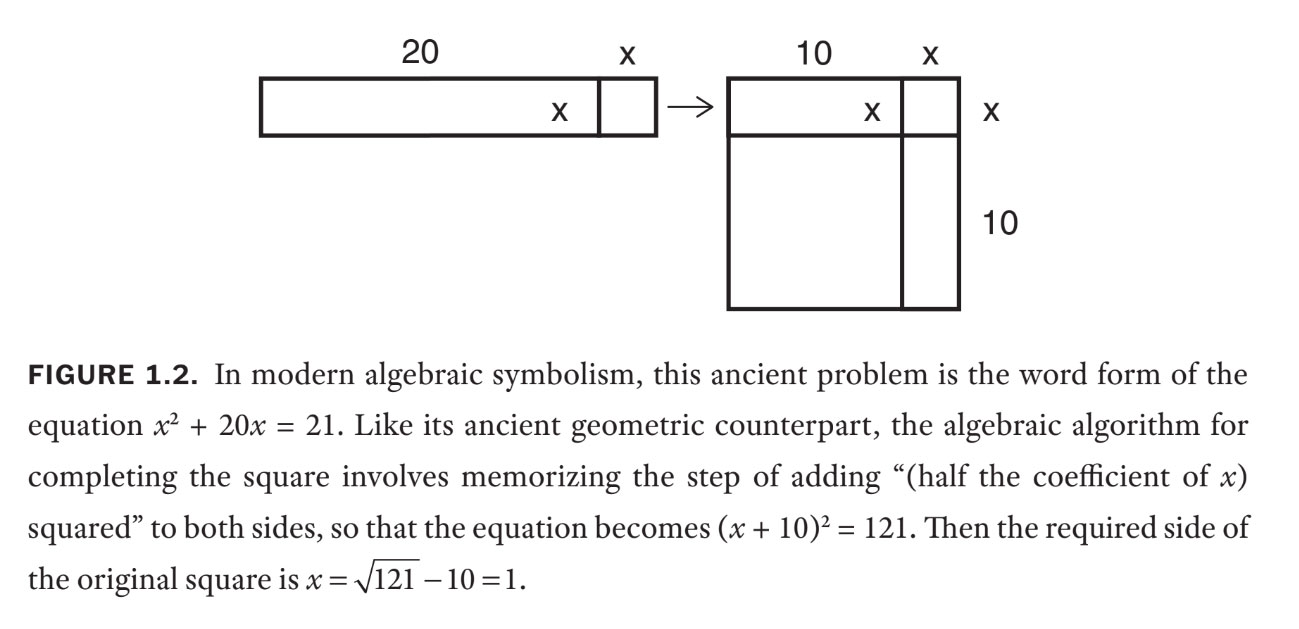
Here isa distinctive instruction problem of the prison term : " tally 20 of my duration to the area of my square , [ to get ] 21 . How substantial is my square ? " This type of trouble , and the algorithm for solving it , is similar to those teach today — except that four millennia ago , the method acting was work out entirely geometrically . First , delineate a square of arbitrary sidex(in modern notation ) ; then add to it a rectangle of dimension 20 [ by]x . Now split this additional rectangle into two adequate smaller ones and coiffure them beside and below the original square . Finally , complete this unexampled , larger square , as in figure 1.2 .
The Mesopotamians had practical problems in intellect when they develop this method , at least initially . last in a land where water was at a premium , their tablets hold in many problems link up to canal and reservoir excavations , the capability of cisterns , the construction and haunt of dams and levees , and administrative accounts relating to these tasks — and to solve these problems , these ancient mathematicians had to solve equation relating to area and volume .

nigh 3,000 years later , Al-Khwārizmī , too , focused on standardized practical problems , and he used a standardised geometrical method acting of complete the foursquare — and so did other mathematician decent up to the 17th century .
This excerption has been edited for style and distance . Reprinted with permission from " Vector : A Surprising Story of Space , Time , and Mathematical Transformation " by Robyn Arianrhod , published by The University of Chicago Press . © 2024 by Robyn Arianrhod . All right reserved .
transmitter : A Surprising Story of Space , Time , and Mathematical Transformation by Robyn Arianrhod is available now — $ 22.71 on Amazon

Algebra is just one of the many slipway we make sense of the numerical macrocosm , and if this excerpt piques your interest , why not delve deeply into the book and discover how something apparently so unsubdivided as a transmitter changed the way we shape blank and even time .