When you buy through tie on our internet site , we may gain an affiliate delegation . Here ’s how it works .
Twenty - five year too former to help oneself Ross get his new couch into his apartment in"Friends,“a mathematician has lastly solve the pestiferous " lounge job . "
The maths problem delineate the largest - size sofa that can match around a corner of a given width — on the dot the problem faced by the case in an episode of " Friends " that beam in 1999 . Ross ' plea of " Pivot ! " could have been avoid , it turns out , if he ’d only considered a Gerver ’s couch with 18 breaking ball sections and a maximal area of 2.2195 units . ( Okay , so maybe it would n’t have been that helpful . )
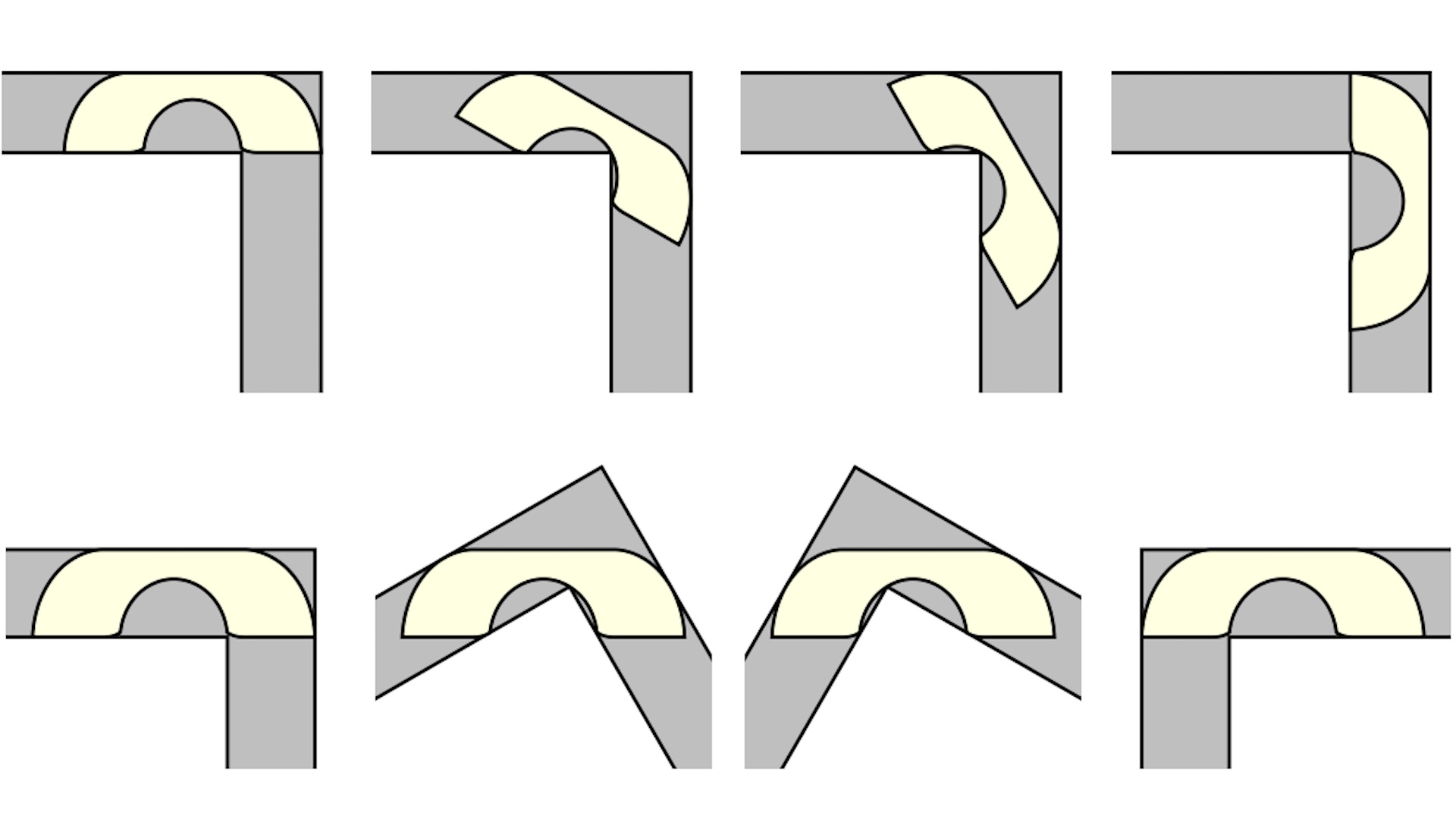
A top-down view of a sofa squeezing around an L-shaped hallway. The strangely-shaped Gerver’s sofa may be the solution to a 60-year-old math conundrum.
The result to the lounge problem is a first for math . The trouble was deposit by Austrian - Canadian mathematician Leo Moser in 1966 . Moser ask for the declamatory possible surface area of a single shape in one planing machine that could move around a right - angled corner of a hallway with a unit breadth of one . While this might seem simple , the mathematics is quite complicated , as the problem necessitate both sphere maximization and movement of the shape .
Now , Jineon Baek , a postdoctoral research worker in mathematics at Yonsei University in South Korea , has arrived at an answer . Baek station his solution on Dec. 2 on the preprint websiteArXiv . In just over 100 page of numerical proof , Baek found that for a hall with a breadth of 1 unit , the imaginary sofa ’s maximal area can be 2.2195 unit — narrowing the answer down with precision from the previously known range of between 2.2195 and 2.37 unit . The proof has not yet been published in a peer - reviewed diary and will necessitate to be lick through by other mathematicians to determine that it is , indeed , optimal .
associate : in high spirits schoolhouse students who come up with ' impossible ' proof of Pythagorean theorem find 9 more solutions to the problem

The " Gerver " of Gerver ’s sofa is mathematician Joseph Gerver , an emeritus prof at Rutgers University whoposited the lower resile of 2.2195 in 1992 . But there had been disputation over whether the sofa could be larger , with a squad in 2018 using a computer - help proof to paint a picture that2.37 was actually the upper adhere .
— Mathematicians get up novel problems to challenge advanced AIs ' abstract thought acquisition — and they failed almost every test
— one C - old ' impossible ' maths problem cracked using the strange natural philosophy of Schrödinger ’s cat

— Mathematicians find 12,000 new solution to ' unsoluble ' 3 - body problem
Gerver ’s sofa is a broad U - regulate couch with a curved " tooshie " that can squeeze around the corner without getting hang up up . The question was whether this painstakingly designed lounge — made of 18 separate curves put together — was really the big , most optimal shape that could make the turn . Baek mold through the geometry of the shape and its motion and found that Gerver ’s solvent was , in fact , right .
The trial impression created a ripple of interest on social media .

" This is the optimal couch , " user@morallawwithinwrote on the social platform X on Dec. 6 , post a motion-picture show of the rather astray - arm lounge chassis . " You may not like it , but this is what flush optimisation take care like . "